
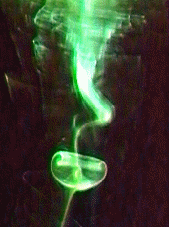
Instabilité de la nappe lors de son enroulement
Eclatement tourbillonnaire
M. Abid, S. Le Dizès, P. Le Gal, C. Lepage, T. Leweke, A.
Verga,
Collaboration: J.-M. Chomaz (LADHYX), D. Barberis & L. Jacquin
(ONERA)
Un problème fondamental de la dynamique des vortex est celui de l'éclatement tourbillonnaire. Il s'agit de la modification brutale de la structure du coeur d'un vortex possédant un écoulement axial. Un tel phénomène est observé sur les tornades ou les tourbillons des ailes d'avion en flèche. Les tourbillons générés par ces ailes résultent du décollement et de l'enroulement d'une nappe de vorticité. Un objectif important est d'établir un lien entre la dynamique de l'enroulement de la nappe de vorticité et la structure du tourbillon résultant. Dans ce projet, nous cherchons à évaluer dans quelle mesure les propriétés des nappes peuvent intervenir dans le processus d'éclatement et comment cela peut être exploité en vue du contrôle de ce phénomène.
Le problème est abordé d'un point de vue théorique, numérique et expérimental. Dans l'étude expérimentale, les nappes sont produites par la mise en rotation d'une plaque plane, initialement au repos, autour d'un de ses côtés. A l'aide d'une plaque triangulaire, l'enroulement se fait de manière conique et un éclatement du tourbillon résultant peut être observé (voir figure). Le développement des perturbations générées par un forçage spatial ou temporel est étudié par la visualisation et la PIV.


Instabilité de la nappe lors de son enroulement
Eclatement tourbillonnaire
Dans l'étude numérique, une résolution des équations basée sur une « méthode vortex » a été mis en oeuvre. Elle vise à déterminer les paramètres qui caractérisent le développement des instabilités de la nappe lors de son enroulement [P1]. Un effort est en particulier fait pour relier la croissance des instabilités au champ d'étirement local de la nappe, notamment pour l'associer aux régions de compression locale. La simulation montre que le régime non-linéaire résultant de la croissance des enroulements secondaires est fortement intermittent et conduit à un spectre d'énergie en k-4 .
Dans le volet analytique, nous nous attachons à comprendre le rôle stabilisateur de l'étirement en cherchant les perturbations optimales qui déstabilisent une nappe plane uniformément étirée. Le gain de la perturbation optimale est comparé à celui des modes de l'instabilité de Kelvin-Helmholtz afin d'évaluer la part des transitoires. Les premiers résultats montrent que ces derniers restent faibles et qu'une approche modale des instabilités de nappe est par conséquent envisageable [P2].
[P1] Abid M., Verga A. Stability of a vortex sheet
roll-up.
Physics of Fluids, 2002 (à paraitre).
[P2] Le Dizès S. Optimal perturbations in stretched
shear layers
Soumis à J. Fluid Mech. Octobre 2002.